11.fejezet: Függvények és külső eljárások
Úgy érzem, éppen itt az ideje, hogy összeszedjünk mindent, amit az eljárásokról, illetve a függvényekről tudni kell és rendszerezzük!
Nos, az alapvető eljárás ugye a main(), ami alapesetben nem ad végeredményt, mivel return 0-val tér vissza. Először is lássunk egy általános függvény-leírást!
típus név ( paraméter1, paraméter2, ...) { törzs }
Itt a következők szerepelnek:
típus: ezt a fajta adatot adja vissza a függvény meghívásakor.
név: ez a függvény elnevezése lesz, azaz így lehet meghívni.
paraméter1, paraméret2, ... (amennyi csak szükséges): minden paraméter tartalmaz egy alapvető típust, mint egy helyi változó deklarációjánál (például: int x); továbbá ezek a változók azonnal használhatók a függvényen belül. Segítségükkel lehet a függvény paraméterek segítségével meghívni. A különböző paramétereket vesszőkkel kell elválasztani.
törzs: ezt kell mindenképpen végrehajtani.
Lássunk erre egy gyakorlati példát!
---------------------------------------------
// függvény-minta
#include <iostream>
using namespace std;
int osszeadas (int a, int b) // ez lesz a függvény neve és ezek a paraméterek
{
int r; // belső változó deklarálása
r=a+b;
return (r); // visszatérési érték megadása
}
int main () // Itt kezdődik a fő-ág.
{
int z; // deklaráció
z = osszeadas (5,3); //Függvény meghívása
cout << "Eredmeny: " << z; // Végeredmény kiírása
return 0;
}
---------------------------------------------
Ezt az összeadást simán meg lehet valósítani a hagyományos "+" jellel is, de így legalább könnyebben meg lehet érteni a C++ függvényeinek működési elvét!
Második példánkban lássunk egy hatványozást, nevezetesen 2-nek a 10-dik hatványát.
Itt magát a külső függvényt 10-szer fogjuk meghívni.
---------------------------------------------
// 2. függvény-minta
#include <iostream>
using namespace std;
float szorzas (float a, float b) // ez lesz a függvény neve és ezek a paraméterek
{
float r; // belső változó deklarálása
r=a*b;
return (r); // visszatérési érték megadása
}
int main () // Itt kezdődik a fő-ág. Ennek muszáj int-nek lennie!
{
float z=1; // deklaráció
for (int n=1; n<11;n++)
{
z = szorzas (z,2); //Függvény meghívása
}
cout << "2^10 = " << z; // Végeredmény kiírása
return 0;
}
---------------------------------------------
Nagyon fontos megérteni, hogy a z változó a main() körében érvényesül, míg az r változó csak a szorzas() körében.
Vannak különleges függvények, amelyek nem adnak vissza értéket. Ezt eljárásnak hívjuk. Neve: void(). Persze ezeknek is lehet paramétere, de nem kötelező!
---------------------------------------------
// Eljárás-minta
#include <iostream>
using namespace std;
void kiiras ()
{
cout << "Eljaras vagyok!";
}
int main ()
{
kiiras();
return 0;
}
---------------------------------------------
Még valami: első látásra furcsának tűnhet, hogy miért kell kirakni a függvény neve után az üres zárójelet, de a C++ lelkivilága ezt megköveteli...
Ebben például nincsen paraméter. Szeretném felhívni a figyelmet arra a tényre, hogy a kiiras(); szabályos, de a kiiras; nem.
Következő példánkban újabb minta jön a C++ végtelen rugalmasságára!
---------------------------------------------
// Paraméterek érték szerinti átadása
#include <iostream>
using namespace std;
void duplaz (int& a, int& b, int& c) // Így a paraméterek értékei megváltoztathatók lesznek!
{
a*=2; // Egyszerű duplázás
b*=2;
c*=2;
}
int main ()
{
int x=1, y=3, z=7;
duplaz (x, y, z);
cout << "x=" << x << ", y=" << y << ", z=" << z;
return 0;
}
---------------------------------------------
Itt, mivel eljárást hívtunk és nem függvényt, így nem lesz egyetlen visszaadott érték.
Ennek ellenére a paraméterek értékét meg tudjuk változtatni, mivel a paraméterek meghívásakor az int után "&" jel került.
A két eljárás-hívást természetesen keverhetjük is! Az alábbi példában egy tetszőleges egész szám szomszédait adjuk vissza (változtatható értékként), míg maga a szám nem változik!
---------------------------------------------
// Számszomszédok
#include <iostream>
using namespace std;
void szamelkov (int szam, int& elozo, int& kovetkezo)
{
elozo = szam-1;
kovetkezo = szam+1;
}
int main ()
{
int x=10, y, z;
cout <<" A szam: " << x;
szamelkov (x, y, z);
cout << ", Elo:zo:=" << y << ", Ko:vetkezo:=" << z;
return 0;
}
---------------------------------------------
Persze lehet olyan kérés is, hogy egy függvény paramétereiben egy vagy több eleve adott értékű legyen. Ez kicsit több mozgásteret tesz lehetővé, mivel így variálhatunk például a paraméterek számával (is). Lássuk a következő példát!
---------------------------------------------
// Alapértelmezett paraméter
#include <iostream>
using namespace std;
int szorzas (int a, int b=2) // b=2 alapértelmezett, ha nem jön meg paraméterként!
{
int r;
r=a*b;
return (r);
}
int main ()
{
cout << szorzas (12); // Nincs megadva a szorzó
cout << endl;
cout << szorzas (20,4); // Itt viszont megadtuk!
return 0;
}
---------------------------------------------
Itt a szorzas() függvény paramétere a szorzandó, amit mindenképpen meg kell adni, valamint a szorzó, amit ha nem adunk meg, akkor a függvény 2-nek veszi.
Többször is láthattuk, hogy a C++ rettenetesen rugalmas - jöjjön hát most egy újabb példa!
---------------------------------------------
// Többszörös elnevezésű függvények
#include <iostream>
using namespace std;
int operate (int a, int b) // Ez egészként lesz végrehajtva.
{
return (a*b);
}
float operate (float a, float b) // Ez pedig valósként.
{
return (a/b);
}
int main ()
{
int x=5,y=2;
float n=5.0,m=2.0;
cout << operate (x,y);
cout << "\n";
cout << operate (n,m);
cout << "\n";
return 0;
}
---------------------------------------------
Itt két különböző függvényt definiáltunk azonos névvel, ám az egyikük csak egész értékeket fogad, míg a másik csak valóst. A fordító a paramétereket áttekintve tudja, hogy melyiket mikor kell hívnia, így nem lesz zavar a meghívásukban. Szeretném mindazonáltal megjegyezni, hogy a függvények ilyen típusú többszörös elnevezésével csínján kell bánni, mivel a visszatérési érték különbözősége mellett legalább egy paraméternek különbözőnek kell lennie!
Következő függvény-típusunk a rekurzív, azaz a saját magát meghívó függvény.
Ennek alapesete a faktoriális. Például: 6! = 1*2*3*4*5*6.
---------------------------------------------
// Faktoriális
#include <iostream>
using namespace std;
long factor (long a)
{
if (a > 1)
return (a * factor (a-1));
else
return (1);
}
int main ()
{
long szam;
cout << "Irjon be egy szamot: ";
cin >> szam;
cout << szam << "! = " << factor (szam);
return 0;
}
---------------------------------------------
Mint látható, sok programozási nyelvvel szemben a C++ logikában alapvetően bent van a rekurzió, azaz a saját függvény sokszoros meghívási lehetősége. A programot futtatva némi próbálkozás után látható, hogy a helyes értéket csak akkor kapjuk meg, ha 0 és 33 közötti egész számot írunk be. Ne feledjük el, hogy a float azért egy viszonylag kis terjedelmű valós számot képes csak tárolni. Nagyobb értékek tárolásához ki kell cserélnünk a típust valami másra, például "long double"-re.
Elő-deklaráció esetén nem kötelező megadni a leendő változók nevét, csak a típusát. Hogy kicsit érthető legyen, lássunk egy példát, ahol mindkettő elő-deklaráció helyes:
int protofuggveny (int first, int second);
int protofuggveny (int, int);
Nézzünk erre egy minta-programot:
---------------------------------------------
// Függvények prototípusának deklarálása
#include <iostream>
using namespace std;
void ps (int a); // Előre megnyugtatom a keresőt, hogy lesz ilyen függvény.
void ptlan (int a);
int main ()
{
int i;
do {
cout << "Kerek egy szamot (0-val kilephet): ";
cin >> i;
ps (i);
} while (i!=0);
return 0;
}
void ptlan (int a) // Íme, itt van az elöl hiányzó függvény.
{
if ((a%2)!=0) cout << "A szam paratlan.\n";
else ps (a);
}
void ps (int a)
{
if ((a%2)==0) cout << "A szam paros.\n";
else ptlan (a);
}
---------------------------------------------
12. fejezet: Gyakorlati feladatok és matematika
Ebben a részben alig-alig lesz új elem, csak a jelenlegi tudásunkat mélyítjük el.
Első feladatként próbáljuk meg a klasszikus másodfokú egyenlet megoldóképletét összehozni.
Matematikai ismétlésként: aki nem tudná, a másodfokú egyenlet általános alakja: ax2+bx+c=0, ahol a,b,c valós számok.
Maga a megoldóképlet pedig:
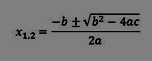
A dologhoz először is úgy érdemes nekilátni, hogy létrehozunk egy önálló eljárást a gyök alatti kifejezés (diszkriminánsnak hívják) kiszámolására.
double diszkr (double a1, double b1, double c1)
{
double dr;
dr = (b1*b1)-(4*a1*c1);
return dr;
}
Érdemes észrevenni, hogy a dr egyetlen sorral simán kiszámítható. Viszont visszatérési értéket kell képezni, mivel függvényként hívjuk meg.
Ha ez megvan, akkor a többi kicsit könnyebb lesz. A kommenteket érdemes elolvasni!
---------------------------------------------
// Másodfokú egyenlet megoldóképlete
#include <iostream>
#include <math.h> // Ez a szükséges matematikai műveleteket tartalmazza
using namespace std;
double diszkr (double a1, double b1, double c1) // Ez a külső függvény, a diszkrimináns kiszámolása
{
double dr;
dr = (b1*b1)-(4*a1*c1);
return dr;
}
int main ()
{
double a,b,c,d,d1,x1,x2; // Hagyományos változók deklarálása
// Adatok bekérése
cout << "Masodfoku egyenlet megoldokeplete." <<endl;
cout << "A'ltalanos formula: ax^2+bx+c=0" <<endl;
cout << "Kerem az 'a' erteket: ";
cin >> a; // a bekérése
cout <<"Kerem a 'b' erteket: ";
cin >> b; // b bekérése
cout <<"Kerem a 'c' erteket: ";
cin >> c; // c bekérése
d = diszkr(a,b,c); // diszkrimináns meghívása
cout <<"\n Diszkriminans erteke: " <<d; // biztonságképpen irassuk ki a disztrmináns értékét
if (d<0)
{
cout <<"\nNegativ szam van a gyo:kjel alatt. Nincs valos megoldas!"; // Ilyenkor nincs megoldás
}
else
{ // Itt lesz megoldás
d1 = sqrt(d); // Gyökvonás
cout <<"\n Gyo:ke: " <<d1; // Biztonsági kiííratás
if (a!=0) // Ha a nevező nem 0, akkor lesz ez az ág aktív
{
x1 = (-b+d1)/(2*a); // Elsö gyök kiszámolása
cout <<"\n x1= " <<x1;
x2 = (-b-d1)/(2*a); // Második gyök kiszámolása
cout <<"\n x2= " <<x2;
}
else
{
cout <<"<nEz nem masodfoku egyenlet!"; //A nevező itt 0
}
}
return 0;
}
---------------------------------------------
Észre kell venni, hogy itt a megszokott "#include <iostream>" mellett egy újabb elem bekerült a program legelejére. Az új elem: "#include <math.h>", melyet azért kellett becsatolni, hogy a matematikai függvényeket, például a gyökvonást is lehessen használni!
Második példánkban írassuk ki a szögek szinuszát 0-tól 360 fokig (5-ösével).
Bár ehhez a legegyszerűbb lenne egy számláló (for-)ciklus, be most pusztán a gyakorlás kedvéért szeretnék hátultesztelő ciklust javasolni!
A kiíratáshoz tudni kell, hogy a sin() függvény három különféle bemenetet, illetve ugyanolyan kimenetet engedélyez. Ezek: float, double, long double.
Még valami: a függvény nem szöget, hanem radiánba átszámolt értékeket kér bemenetként. Ehhez a szög értékét meg kell szorozni a PI értékével, illetve el kell osztani 180-cal. A kész függvény-kódban érdemes volt előre definiálni a PI értékét, mert így nem kell vele később foglalkozni!
Tehát a teljes kód:
---------------------------------------------
// Szinusz-példa
#include <iostream>
#include <math.h>
using namespace std;
#define PI 3.14159265
int main ()
{
long double i=0, j;
do
{
j = sin(i*PI/180);
cout <<"\n sin(" <<i <<")= " <<j;
i += 5;
}
while (i<361);
return 0;
}
---------------------------------------------
Gyakorlati javaslat: ha az adott nyelvben nincsen direkt átszámító függvény fokról radiánba, illetve vissza, akkor érdemes ezt külső függvényként külön definiálni.
További matematikai függvények a math.h könyvtárban:
(Forrás: http://www.cplusplus.com/reference/clibrary/cmath/ )
Trigonometrikus függvények:
cos cosinusz
sin sinusz
tan tangens
acos arcus cosinusz
asin arcus sinusz
atan arcus tangens
atan2 arcus tangens két paraméterrel (radiánban, kér koordinátával adja vissza a -pi +pi értékek között)
Hiperbolikus függvények:
cosh cosinusz hiperbolikusz
sinh sinusz hiperbolikusz
tanh tangens hiperbolikusz
Exponenciális és logaritmikus függvények:
exp Exponenciális (e hatványa), ahol e=2,71828.
frexp Egy hátványt felbont valós szorzóra és 2 egész kitevőjű hatványára.
ldexp Előzőhöz hasonló, csak eltérő lehetőségekkel
log Egy szám természetes (azaz e-alapú) logaritmusát adja meg.
log10 10-alapú logaritmus.
modf Egy szám felbontása egész és törtrészre.
Hatvány-függvények:
pow Egy szám hatványa (Paraméterek: alap,kitevő)
sqrt Négyzetgyök
Vegyes függvények:
ceil A legkisebb egész szám, ami nem kisebb, mint a paraméter.
fabs Abszolút érték
floor A legnagyobb egész szám, ami nem nagyobb, mint a paraméter.
fmod Osztási maradék